Structure from Motion (SfM)

Overview

Structure from Motion (SfM) is a computer vision technique for reconstructing 3D structures from 2D image (sequencial and/or non-sequencial). This project demonstrates the end-to-end pipeline for SfM, including feature detection, camera pose estimation, triangulation, and 3D point cloud generation with code, its mathematical representation and some open source tools to generate this.

Notation Legend

Before diving into the technical details, let’s establish our notation:

• $\mathbf{x}$: 2D image coordinates (homogeneous)
• $\mathbf{X}$: 3D world coordinates
• $K$: Camera intrinsic matrix
• $R$: Rotation matrix
• $t$: Translation vector
• $\pi$: Projection function

SfM Pipeline: Mathematical Foundations

1. Camera Model: Geometric Projection

The pinhole camera model mathematically represents how 3D world points are mapped to 2D image planes.

Projection Equation: $\mathbf{x}=K[R|t]\mathbf{X}$

Computational Insights:

• Complexity: $O(1)$ projection operation
• Requires pre-calibration of intrinsic parameters
• Assumes perfect pinhole camera geometry

Practical Implementations:

• OpenCV Camera Calibration
• COLMAP Camera Modeling
• Bundler Toolkit

2. Feature Detection: Identifying Distinctive Image Landmarks

Feature detection creates a bridge between 2D images by identifying robust, invariant points.

Feature Representation: Let ${\mathbf{f}}_i$ represent a feature point with descriptor $D({\mathbf{f}}_i)$

Popular Algorithms:

1. SIFT (Scale-Invariant Feature Transform)
   • Invariant to: Scale, Rotation, Illumination
   • Computational Complexity: $O(n\log n)$

1. ORB (Oriented FAST and Rotated BRIEF)
   • Real-time performance
   • Computational Complexity: $O(n)$

Descriptor Distance Metric: $\text{Similarity}(D({\mathbf{f}}_i),D({\mathbf{f}}_j))=\frac{\sum _{k=1}^D|d_i^k-d_j^k|}{D}$

3. Feature Matching: Establishing Correspondences

Matching features across images requires robust correspondence algorithms.

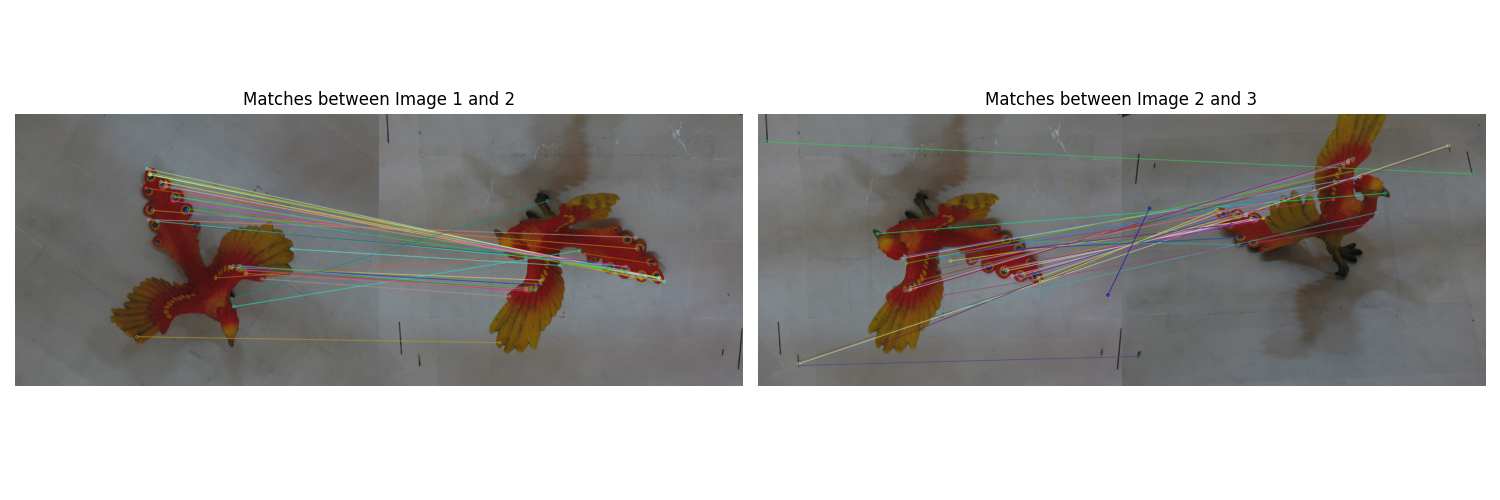
Matching Strategies:

• K-Nearest Neighbor (KNN)
• RANSAC for outlier rejection
• Lowe’s ratio test for robust matching

Mathematical Formulation: $\text{Match}({\mathbf{f}}_i,\mathbf{f}j)=\mathrm{argmin}m\in M|\mathbf{D}({\mathbf{f}}_i)-\mathbf{D}({\mathbf{f}}_j){|}_2$

4. Fundamental Matrix Estimation

The Fundamental Matrix captures geometric relationships between image pairs.

Epipolar Constraint: ${\mathbf{x}}_j^T\mathbf{F}{\mathbf{x}}_i=0$

Estimation Methods:

• Eight-point Algorithm
• Linear Least Squares
• Non-linear Refinement

Computational Complexity: $O(n³)$ for SVD-based estimation

5. Essential Matrix Decomposition

Bridges geometric relationships with camera motion.

Derivation: $\mathbf{E}=K^T\mathbf{F}K$

Motion Decomposition: $\mathbf{E}=\mathbf{R}[\mathbf{t}{]}_{\times }$

6. Triangulation: 3D Point Reconstruction

Converts 2D correspondences to 3D point clouds.

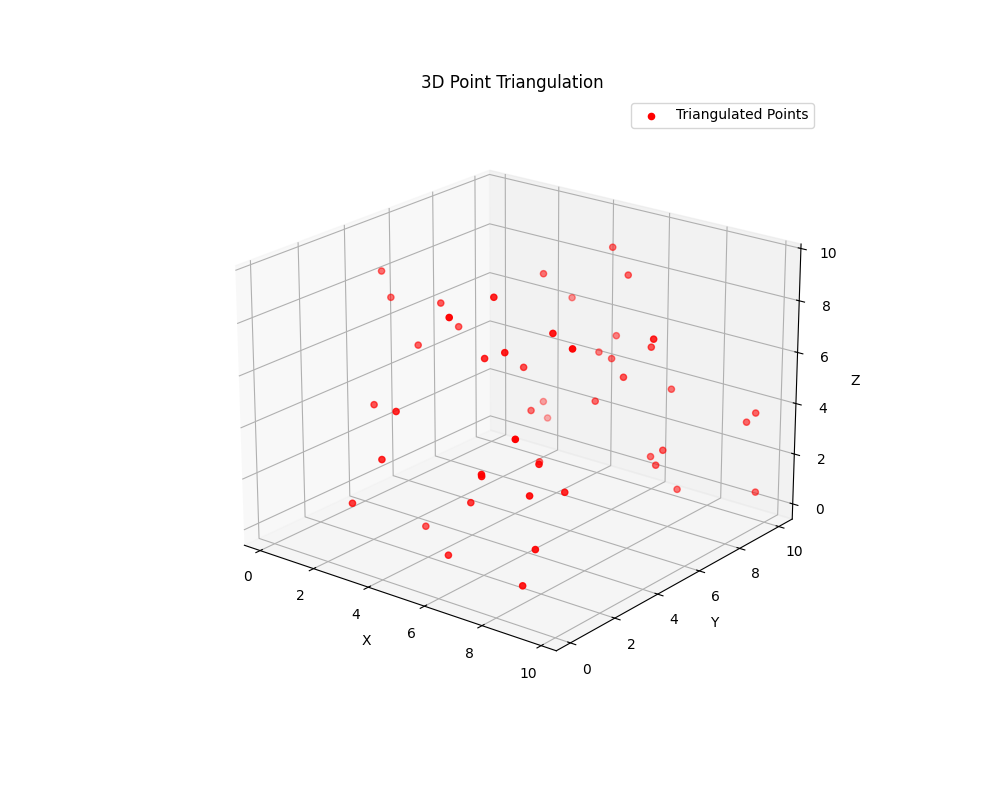
Linear Triangulation: $\mathbf{A}\mathbf{X}=0$

Where: $\mathbf{A}=\left[\begin{array}{c}{\mathbf{x}}_1\times P_1\\ {\mathbf{x}}_2\times P_2\end{array}\right]$

Triangulation Algorithms:

• Direct Linear Transformation (DLT)
• Iterative Refinement
• Geometric Error Minimization

7. Bundle Adjustment: Optimization

Refines camera parameters and 3D point locations simultaneously.

Objective Function: $\underset{K,R,t,\mathbf{X}}{min}\sum _{i,j}\Vert {\mathbf{x}}_{ij}-\pi (K,R_j,t_j,{\mathbf{X}}_i){\Vert }^2$

Optimization Techniques:

• Levenberg-Marquardt Algorithm
• Gauss-Newton Method
• Computational Complexity: $O(n³)$

8. Sparse Point Cloud Generation

Aggregates triangulated points into an initial 3D representation.

9. Dense Reconstruction

Enhances sparse point clouds with per-pixel depth estimation.

Depth Estimation: $z=\arg \underset{z}{min}\sum _i\Vert I_i(u,v)-I_j(\pi (u,v,z)){\Vert }^2$

Advanced Techniques:

• Multi-View Stereo (MVS)
• Depth Fusion Algorithms
• Probabilistic Depth Estimation

Practical Considerations

• Choose feature detectors based on computational resources
• Validate camera calibration
• Handle image noise and computational constraints
• Use robust optimization techniques

Recommended Tools

• COLMAP
• OpenSfM
• VisualSfM
• Bundler

Conclusion

Structure from Motion represents a powerful intersection of geometric algebra, optimization, and computer vision, transforming 2D image sequences into rich 3D representations.